Rules For Horizontal Asymptote
Horizontal Asymptote Rules: Before pulling into the interpretation of a horizontal asymptote, let’s first go over what a function is. A function is an equation that tells you how two things relate. Regularly, functions tell you how y is ascribed to x. Functions are often graphed to contribute a visual. Given a particular function, there is actually a 2-step procedure we can use to find the horizontal asymptote. Learn what that is in this practice along with the rules that horizontal asymptotes pursue.
A horizontal asymptote is a straight line that tells you how the business will behave at the very perimeters of a graph. A straight asymptote is not sacred ground, however. The function can touch and even cross over the asymptote. Horizontal asymptotes exist for business where both the numerator and denominator are polynomials. These functions are called levelhead expressions. Let’s look at one to see what a straight asymptote looks like.

Rules Horizontal Asymptote
Whereas steep asymptotes are sacrosanct ground, horizontal asymptotes are just useful suggestions.
Whereas you can never touch a steep asymptote, you can (and often do) touch and even cross horizontal asymptotes.
Whereas vertical asymptotes indicate very specific behavior (on the graph), usually close to the origin, horizontal asymptotes point out general behavior, usually far off to the sides of the graph.
In other words, straight asymptotes are different from vertical asymptotes in some fairly significant ways.
To understand the concept of horizontal asymptotes, let’s look at a few examples.
-
Find the horizontal asymptote of the following function:
First, notice that the denominator is a sum of squares, so it doesn’t factor and has no real zeroes. In other words, this rational function has no vertical asymptotes. So we’re okay on that front.
As mentioned above, the horizontal asymptote of a function (assuming it has one) tells me roughly where the graph will being going when x gets really, really big. So I’ll look at some very big values for x; that is, at some values of x which are very far from the origin:
|
x |
y = \dfrac{x + 2}{x^2 + 1}
|
|
–100 000 |
–0.0000099… |
|
–10 000 |
–0.0000999… |
|
–1 000 |
–0.0009979… |
|
–100 |
–0.0097990… |
|
–10 |
–0.0792079… |
|
–1 |
0.5 |
|
0 |
2 |
|
1 |
1.5 |
|
10 |
0.1188118… |
|
100 |
0.0101989… |
|
1 000 |
0.0010019… |
|
10 000 |
0.0001000… |
|
100 000 |
0.0000100… |
Off to the sides of the graph, where x is strongly negative (such as –1,000) or else strongly positive (such as 10000) the “+2” and the “+1” in the expression for y really don’t matter so much. I ended up having a really big number divided by a really big number squared, which “simplified” to be a very small number. The values of y came mostly from the “x” and the “x2“, especially once x got very large. And since the x2 was “bigger” than the x, the x2 dragged the value of the whole fraction down to y = 0 (that is, down to the x-axis) when x got big.
This makes perfect sense, when you think about it. If you’ve got a zillion (plus two, but who cares about that?) divided by a zillion squared (plus 1, but who cares about that?), then you’ve essentially got a zillion divided by the square of a zillion, which simplifies to 1 over a zillion. Which is very, very small. So of course the value of the function gets very, very small; namely, it gets very, very close to zero.
Horizontal Asymptote Degree Rules

Remember that an asymptote is a line that the graph of a function approaches but never touches. Rational functions contain asymptotes, as seen in this example:
In this example, there is a vertical asymptote at x = 3 and a horizontal asymptote at y = 1. The curves approach these asymptotes but never cross them.
The method used to find the horizontal asymptote changes depending on how the degrees of the polynomials in the numerator and denominator of the function compare.
If both polynomials are the same degree, divide the coefficients of the highest degree terms.
Example:
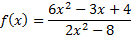
Both polynomials are 2nd degree, so the asymptote is at 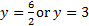
If the polynomial in the numerator is a lower degree than the denominator, the x-axis (y = 0) is the horizontal asymptote.
If the polynomial in the numerator is a higher degree than the denominator, there is no horizontal asymptote. There is a slant asymptote, which we will study in a later lesson.
Rules For Finding Horizontal Asymptote
I’ll start by showing you the traditional method, but then I’ll explain what’s really going on and show you how you can do it in your head. It’ll be easy!
Given some polynomial guy

| If |
, then the x-axis is the horizontal asymptote. | ||
| If
|
, then the horizontal asymptote is the line |
||
| If |
, then there is no horizontal asymptote. (There is a slant diagonal or oblique asymptote.) |
Yeah, yeah, you COULD just memorize these things… but it’s way better to KNOW what’s going on. Then you can just do it.
What we’re really doing is some quick long division to divide the denominator into the numerator. The cool thing is that we only need to do the first part — no remainder crud! And we can do it in our heads!
Horizontal Asymptote Rules Rational Functions
The roots, zeros, solutions, x-intercepts (whatever you want to call them) of the rational function will be the places where p(x) = 0. That is, completely ignore the denominator. Whatever makes the numerator zero will be the roots of the rational function, just like they were the roots of the polynomial function earlier.
If you can write it in factored form, then you can tell whether it will cross or touch the x-axis at each x-intercept by whether the multiplicity on the factor is odd or even.
An asymptote is a line that the curve approaches but does not cross. The equations of the vertical asymptotes can be found by finding the roots of q(x). Completely ignore the numerator when looking for vertical asymptotes, only the denominator matters.
If you can write it in factored form, then you can tell whether the graph will be asymptotic in the same direction or in different directions by whether the multiplicity is even or odd.
Asymptotic in the same direction means that the curve will go up or down on both the left and right sides of the vertical asymptote. Asymptotic in different directions means that the one side of the curve will go down and the other side of the curve will go up at the vertical asymptote.
A horizontal line is an asymptote only to the far left and the far right of the graph. “Far” left or “far” right is defined as anything past the vertical asymptotes or x-intercepts. Horizontal asymptotes are not asymptotic in the middle. It is okay to cross a horizontal asymptote in the middle.
The location of the horizontal asymptote is determined by looking at the degrees of the numerator (n) and denominator (m).
- If n<m, the x-axis, y=0 is the horizontal asymptote.
- If n=m, then y=an / bm is the horizontal asymptote. That is, the ratio of the leading coefficients.
- If n>m, there is no horizontal asymptote. However, if n=m+1, there is an oblique or slant asymptote.
Sometimes, a factor will appear in the numerator and in the denominator. Let’s assume the factor (x-k) is in the numerator and denominator. Because the factor is in the denominator, x=k will not be in the domain of the function. This means that one of two things can happen. There will either be a vertical asymptote at x=k, or there will be a hole at x=k.
Let’s look at what will happen in each of these cases.
- There are more (x-k) factors in the denominator. After dividing out all duplicate factors, the (x-k) is still in the denominator. Factors in the denominator result in vertical asymptotes. Therefore, there will be a vertical asymptote at x=k.
- There are more (x-k) factors in the numerator. After dividing out all the duplicate factors, the (x-k) is still in the numerator. Factors in the numerator result in x-intercepts. But, because you can’t use x=k, there will be a hole in the graph on the x-axis.
- There are equal numbers of (x-k) factors in the numerator and denominator. After dividing out all the factors (because there are equal amounts), there is no (x-k) left at all. Because there is no (x-k) in the denominator, there is no vertical asymptote at x=k. Because there is no (x-k) in the numerator, there is no x-intercept at x=k. There is just a hole in the graph, someplace other than on the x-axis. To find the exact location, plug in x=k into the reduced function (you can’t plug it into the original, it’s undefined, there), and see what y-value you get.
Leave a Reply